ic: images, text, markdown fixes
This commit is contained in:
parent
0e188b20f6
commit
ee2e099d67
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(1)</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(2)</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(4)</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(6)</center>
|
||||
|
||||
@ -12,7 +12,7 @@ The essence of the problem is that Schrödinger's wave function, used to describ
|
||||
|
||||
Thus, a quantum object, when viewed from the classical world, always appears as a simultaneous collection or superposition of incompatible states. Due to this fundamental ambiguity, any measurement of a quantum object's state cannot be predicted precisely and only provides probabilistic values. Yet, the wave function itself is quite deterministic — in terms of complex numbers.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(7)</center>
|
||||
|
||||
@ -44,7 +44,7 @@ Overall, such a radical revision of traditional scientific views on reality was,
|
||||
|
||||
But without the author himself, who was disappointed with his colleagues' reaction to his discovery. Immediately after defending his dissertation, Hugh Everett essentially parted ways with the "queen of physics" forever. [i5]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>([Read more](/tbc/32/))</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(9)</center>
|
||||
|
||||
@ -10,7 +10,7 @@ All that is known on this matter today can only be gleaned from the memoirs of p
|
||||
|
||||
There are also a few brief but extremely inspired letters from Pauli, where the essence of his great insight is conveyed by words like: "**Division and reduction of symmetry, this is the kernel of the brute!**… Now we are on the trail!". [o10]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(10)</center>
|
||||
|
||||
@ -20,7 +20,7 @@ To make it clearer what is being discussed here, it should be reminded that for
|
||||
|
||||
To put it more poetically, the scientist was searching for ways to return to the modern scientific conception of the world the ancient notion of the "soul of matter". A notion commonly accepted in antiquity, but completely lost over the last 300 years. [i8]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(11)</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(12)</center>
|
||||
|
||||
@ -26,7 +26,7 @@ As a juggler practitioner, he even attempted to master a peculiar juggling techn
|
||||
|
||||
Another interesting work by Shannon in the same vein was a "philosophical" sculpture depicting a juggler tossing other, smaller jugglers, who, in turn, juggled even smaller jugglers…
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(14)</center>
|
||||
|
||||
@ -38,7 +38,7 @@ Another striking example of the same series was a specialized minicomputer const
|
||||
|
||||
In short, if you look at all these unserious entertainments of Claude Shannon from a slightly different, physico-theoretical perspective, linking them with the studies of Everett and Pauli, you can discover rather interesting things.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>([Read more](/tbc/41/))</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(15)</center>
|
||||
|
||||
@ -14,7 +14,7 @@ The movement of a point generates a 1-dimensional line, specifically, a straight
|
||||
|
||||
Similarly, 3-dimensional space can be generated by parallel translation of a plane or rotation of a plane around one of its lines. It is clear that this process can be developed further – towards the generation of spaces of higher dimensions.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(16)</center>
|
||||
|
||||
@ -22,7 +22,7 @@ The idea of rotation is embedded in the foundations of mechanics and geometry fr
|
||||
|
||||
The equation describing the motion of a point in such a system, as it turned out, is equally suitable for describing the oscillations of a weight on a spring or a pendulum on a suspension, for the sinusoidal propagation of waves, and for describing the modes of string vibrations. Due to obvious connections with music, the system is called a harmonic oscillator.
|
||||
|
||||
<center>")</center>
|
||||
")
|
||||
|
||||
When classical physics was replaced by quantum physics, it quickly became apparent that the harmonic oscillator plays no lesser role there. More precisely, a much greater one. Not only because the strictly discrete natural frequencies of a musical string's sound are a direct mechanical analogy for the allowed orbitals of an electron in an atom. But also because the wave equations of quantum objects are fundamentally built on the idea of oscillations and the mathematics of complex numbers. And this mathematical apparatus is essentially ideally suited for solving problems about the motion of a point in a circle (in the phase space of states).
|
||||
|
||||
@ -34,7 +34,7 @@ Thus, in classical mechanics, the "Foucault's pendulum" – the rotation of the
|
||||
|
||||
When – in the 19th century – the tools of multidimensional geometry began to be included in the standard arsenal of mathematics, the most curious researchers began to tackle the problems of perception. In other words, long before the appearance of the concept of 4-dimensional space-time, work began to be devoted to how an observer from, say, a 2-dimensional world would perceive 3-dimensional objects. [o16]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
One of the most characteristic examples of this kind is the passage of a 3-dimensional sphere through a flat world. To the inhabitants of the plane, it would initially appear as a tiny point, then a circle of variable – first growing, then decreasing – diameter, and finally again as a vanishingly small point. Using this analogy, it is significantly easier to imagine that a 4-dimensional sphere passing through a 3-dimensional world like ours would appear as a spherical object with a size changing from zero to a maximum diameter.
|
||||
|
||||
@ -42,7 +42,7 @@ From this picture, it is logical to move on to constantly oscillating quantum pa
|
||||
|
||||
Another important aspect of the quantum world is that particles of matter interact – quantum entangle – not directly but necessarily through a photon or a mediator particle. For the geometric description of this picture, it is essential that a moving photon can be represented by its plane of polarization. Typically, if a photon is reflected by a particle, the plane of the wave propagates without rotation (linear polarization). But if the photon is emitted by a particle, then the plane of polarization rotates around the axis of propagation (circular polarization).
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Looking at the picture from this perspective, it is easier to imagine the mechanism of forming quantum entanglement. When a photon departs from one particle, they are already entangled, and the photon's plane of polarization already carries information about the quantum state (spin direction) of the particle. When the photon reaches another particle, the plane of polarization makes a "slice" of its current state. If the particle’s diameter is maximum, then the interaction takes place at its maximum. And if the cross-section diameter is zero at that moment, then there is no interaction and, consequently, no entanglement at all.
|
||||
|
||||
@ -72,7 +72,7 @@ If we recall that Hugh Everett built his concept on Shannon's theory of informat
|
||||
|
||||
In an ultra-brief formulation, this idea is since some time expressed by the maxim "**It from bit**" . And it is unlikely a coincidence that such a beautiful aphorism was invented – at the end of his long life – by John Archibald Wheeler [i12]. The teacher of Feynman and Everett, who managed to outlive his students by several decades.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>([Read more](/tbc/42/))</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(19)</center>
|
||||
|
||||
@ -6,7 +6,7 @@ The theoretical construction of the multiverse in Hugh Everett's dissertation wa
|
||||
|
||||
One notable feature of the Dirac equation is that it can be written in a unique form, sometimes referred to as the zigzag representation of a spinor [o19]. In this description, every electron (or another massive fermion with spin 1/2) appears as a particle moving along a zigzag trajectory and is in a state of continuous oscillations between the left-handed "zig" phase and the right-handed "zag" phase. Each of these alternating states, by itself, is massless, and mass arises only when the entire scenario is considered collectively.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>Zigzag representation of an electron (from R. Penrose's book "The Road to Reality")</center>
|
||||
|
||||
@ -32,13 +32,13 @@ The still poorly studied physics of granular media [i18] — sand, powders, susp
|
||||
|
||||
Speaking more specifically about oscillons, the main feature of this variety of waves in a granular medium is their rare stability. Once arisen, this solitary wave can rise and fall, maintaining its identity indefinitely long—as long as the experiment lasts.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>Oscillation phases of oscillon</center>
|
||||
|
||||
Another equally important feature of oscillons is the specificity of their interaction, explicitly referring to the long-standing Bjerknes’ theory of pulsations. Being in the same phase of oscillation, oscillons repel each other, and being in opposite phases, they attract each other.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Putting the facts slightly differently, the new discovery has revealed remarkable possibilities. By combining oscillons with Bjerknes’ theory, a clear and comprehensible explanation emerges — not only for well-known phenomena (which are explained in textbooks rather clumsily), but also for the still-mysterious secrets of electricity and magnetism.
|
||||
|
||||
@ -58,7 +58,7 @@ In the fourth dimension — time — our entire world, as is well known, constan
|
||||
|
||||
In mathematical terminology, a situation when all orientation directions of elements were previously equal — or symmetric — and then became consistently oriented in one direction, is called "symmetry breaking."
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
In classical physics, a very fitting example of this phenomenon is provided by the phenomenon of antiferromagnetism. Like other substances with magnetic properties, antiferromagnets consist of molecules with a dipole moment that behave like tiny magnets. At high temperatures, all these little magnets are oriented randomly within the substance, meaning that every direction is equally probable, and the entire system as a whole is symmetrical.
|
||||
|
||||
@ -68,7 +68,7 @@ Juxtaposing this picture of spontaneous symmetry breaking with the phenomenon of
|
||||
|
||||
Formulating more precisely, it would be more accurate to speak of the electron not as a "hilltop" but as the lower point of a conical "pit" of the oscillon. Because in conditions of a double membrane, constantly in a state of vibrations, phases of the oscillon like "hill" turn out to be less stable and perform the role of anti-particles. That is, they disappear as a result of annihilation. Such a pair of membranes vibrating in antiphase is commonly named in modern physics as a "brane-antibrane" system.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Thus, on a pair of membranes, only the stable version of oscillons remains — in the form of a conical "pit" (the proton) and its "bottom" in the form of a point-like microvortex (the electron), synchronously jumping from one surface to the other—along the time axis [i16]
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(23)</center>
|
||||
|
||||
@ -18,7 +18,7 @@ Not to mention that, on a theoretical level, no one has yet succeeded in beautif
|
||||
|
||||
But before delving into the peculiarities of the mechanism connecting quantum gravity and quantum entanglement in the model, it is useful to consider several important ideas and consequences that arise from the overall two-brane construction. One central idea here is the **concept of the universe as a closed one-sided surface**. The simplest example of one-sided surface is the **Möbius strip**. [i21][i22]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Accordingly, the world as a Möbius strip is the simplest and most natural explanation for why the number of positive and negative electric charges in the universe is always equal. So the total electric charge of the universe remains invariably equal to zero.
|
||||
|
||||
@ -56,7 +56,7 @@ Soon after, in 2001, an essentially similar experimental result emerged. In lase
|
||||
|
||||
Studies of nonlinear optics phenomena are vital on their own and particularly interesting for sharing many similarities with the physics of quantum superfluids like Bose-Einstein Condensates. Specifically, the behavior of quantum vortices in BECs and laser optics is described by similar equations.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>Process of the dynamical inversion of the topological charge</center>
|
||||
|
||||
@ -66,7 +66,7 @@ As laser experiments have shown, once a spirally twisted light beam passes throu
|
||||
|
||||
A notable feature in the mechanism of an optical vortex or "topological charge" inversion is the experimentally observed phase where it extends into a thin line or vortex tube.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
This result is particularly fascinating for two reasons. First, as the image of this phenomenon evidently resembles astronomical images of spiral galaxies with a bar in the core. This same concept—using the metaphor of a spinning "garden sprinkler"—often appears in popular explanations for a range of physical theories, from nuclear physics to superstrings and quantum gravity. [i28]
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(27)</center>
|
||||
|
||||
@ -34,13 +34,13 @@ In other words, at the moment of convergence of the branes, the tube's axis is p
|
||||
|
||||
Here, to complete the picture, it remains to find in the phase of brane convergence also the fermionic partner for each quantum of light or single photon. For this, it is time to recall that unusual particles are emitted from both ends of the vortex tube during the brane convergence. One of them – the tachyon leaving the membrane – should be given a separate section further, while the second particle, eventually having the hallmark of a graviton (spin 2) and consisting of what seems like two parts – with a "longitudinally divided mode" – is exactly what is needed for SUSY. [i33]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>Kelvin Oval (left) and vortex ring in section</center>
|
||||
|
||||
There is reason to believe that at the phase of maximum brane convergence, this particle appears as a pair of flat identical vortices rotating in opposite directions – like a vortex ring "in section". This configuration is known in physics as the "Kelvin Oval" [i34], has soliton properties – a stable solitary wave – and is most famous for propagating strictly in a straight line as a single entity. During the branes convergence the axes of rotation of the vortices in this pair are perpendicular to the membrane, so geometrically they should be considered fermions at this moment.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
And remarkably, the total spin of this pair of vortices with an antiparallel combination of rotation axes sums up from the values (+1/2) and (–1/2). That is, equal to zero – as with the **Higgs boson**, whose influence is presumed in the Standard Model to be responsible for **generating the inert mass of quantum particles**…
|
||||
|
||||
@ -68,7 +68,7 @@ Other substantial details in Randall and Sundrum, however, look different. But h
|
||||
|
||||
In the RS model, it is assumed that only the 3 known interactions of quantum physics operate on our brane, while all gravity is concentrated on the second membrane, called the "gravitybrane." Calculations of the model based on General Relativity showed that the energy of the branes in this situation curves the fifth dimension extremely strongly, giving the entire structure very specific features.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
In essence, the strongest changes in sizes, masses, and even the flow of time that occur in this two-brane configuration when shifting through the fifth dimension are very reminiscent of the powerful space-time deformations near cosmic black holes. However, if we assume that particles from the Standard Model physics are located on one of the branes, then according to calculations, they inevitably must have a small mass. This result means that, in principle, the hierarchy problem could be solved in a completely natural and automatic way…
|
||||
|
||||
@ -84,7 +84,7 @@ Moreover, the Randall-Sundrum model also contains – albeit implicitly – an i
|
||||
|
||||
Each of the two branes at the edges of the RS model is similar to the world familiar to humans – flat space without any special gravitational curvature effects. Moreover, the same picture is characteristic of any layer given by a slice of space through any point along the fifth dimension axis. All layers also have flat geometry.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
However, as a whole all these 4d-layers are glued to each other so that the five-dimensional space is very strongly curved. That is, **when transitioning in the fifth dimension from one layer to another, the scales of sizes, locations, time, mass, and energy change significantly**. But although the values of masses for particles vary greatly depending on the position in the fifth dimension, all physics invariably continues to appear 4-dimensional…
|
||||
|
||||
@ -124,7 +124,7 @@ And if the extremely non-trivial geometry at the core of this model and string t
|
||||
|
||||
And since the compactified, in principle unattainable micro-spaces of string theory now turn out to be the same as our macrouniverse, only with a previously hidden structure, very interesting prospects open up.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Calabi-Yau spaces are famous for extremely intricate configurations of geometry with many holes and transitions. And **in topology, any hole means an alternative shortest path from one point of space to another**. In other words, along with the new map of the universe, the perspective of fast travels to previously unthinkable distances simultaneously appears. We just need to learn how to move along frequency layers…
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(31)</center>
|
||||
|
||||
@ -20,7 +20,7 @@ The last of the mentioned species of well-known quasiparticles – anyons – de
|
||||
|
||||
The remarkable properties of anyons are important for several reasons. Firstly, because due to relativistic effects impacting the body of a very rapidly rotating proton, there are reasons to believe that a spherical particle can take the shape of a flat disk. And for the particle-components of the proton, rotating inside this energy vortex, unclear quantum properties are characteristic. Quarks are not quite fermions, gluons – not quite bosons.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>Hyde's Vacillation</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(36)</center>
|
||||
|
||||
@ -48,7 +48,7 @@ According to theoretical estimates, this layered structure of a stable tachyonic
|
||||
|
||||
This skeleton, formed by "fibers of the soul," looks like one-dimensional only locally. However, in general, it is organized into a single global structure. On the one hand, this **giant network penetrates and encompasses all space-time**. On the other hand, it somewhat **resembles the structure formed by neurons in the human brain**…
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Completely independently of these works, a renowned theorist and Nobel laureate Frank Wilczek put forward his own set of substantive ideas in early 2012 about a specific physics-mathematics framework, one that continuously generates threads of matter’s memory in the form of crystalline structures. In particular, Wilczek demonstrated that both in classical and quantum mechanical descriptions of our world, it is possible — as it turns out — to construct crystal structures in the 4th dimension, that is, in time, in a consistent and mathematically grounded way. [o36]
|
||||
|
||||
@ -80,7 +80,7 @@ To vividly demonstrate the connections between the Riemann Hypothesis and the my
|
||||
|
||||
By carefully reformulating the Riemann Hypothesis into a series of weaker statements, Matiyasevich used a computer program to calculate and plot on the complex plane the trajectories of certain characteristics-iterations, collectively painting a picture of the "hidden life of the Riemann function."
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
In these graphs, two classes of objects are distinctly visible, located on different sides of the critical line-divider passing parallel to the imaginary axis through the point 1/2. The objects on the left were named "electrons" by the author since their trajectories resemble those of particles colliding and diverging. The objects on the right behave differently, resembling twisted double spirals, and were named "trains" by Matiyasevich.
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(41)</center>
|
||||
|
||||
@ -10,7 +10,7 @@ For the same phenomenon or object, there are several significantly different des
|
||||
|
||||
A fundamentally important detail of this problem is the intentional words "appears to be" and "impression." The importance of this nuance can be illustrated by the example of the so-called "wave-particle duality" of quantum particles – perhaps the most famous natural phenomenon with a dual description of its physical properties.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
If we look more closely at the birth and establishment of this fundamental "duality" in science, it's not too difficult to notice the following. Had historical circumstances been slightly different, and if the wave (de Broglie and Schrödinger) views on quantum mechanics had gained a dominant role, the overall picture might have turned out to be far more coherent and comprehensible.
|
||||
|
||||
@ -18,7 +18,7 @@ The strange "paradoxes of duality" in the physics of quantum objects, which beha
|
||||
|
||||
Since the 19th century, hydrodynamics has known the so-called solitary waves (solitons), whose behavior largely corresponds to the nature of particles [i50]. Why this happened is a different long story [i51], but scientists began seriously studying the physics of wave solitons only a century later, starting in the 1960s. In other words, when quantum physics, based on an alternative concept of particles, had long been in a state of maturity and triumphant success.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>Train of solitons in a Bose-Einstein condensate</center>
|
||||
|
||||
@ -90,7 +90,7 @@ Therefore, a far more promising endeavor seems to be something else. Take a clos
|
||||
|
||||
An aspect of holography, which is quite significant but has been practically untouched so far, is the principle of self-similarity. Due to the peculiarities of recording wave information in a hologram, any fragment of a holographic snapshot — in contrast to a photograph—reproduces the entire image as a whole, only with possibly fewer details.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>The boundary of the Mandelbrot set with successive magnification of image fragments serves as an example of the holographic principle in the geometry of complex numbers.</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(46)</center>
|
||||
|
||||
@ -18,7 +18,7 @@ For Descartes's worldview, it seems, the symbol of the tree appeared more relata
|
||||
|
||||
The hierarchical **structure for the general complex of human knowledge** about the world — i.e., for "philosophy" in Descartes's terminology — should, in his opinion, look as follows: "All philosophy is **like a tree**, of which Metaphysics is the root, Physics the trunk, and all other sciences the branches that grow out of this trunk, which are reduced to three principals, namely, Medicine, Mechanics, and Ethics."
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Let us ignore the obvious archaism, so to speak, of Descartes's classification of sciences, and focus only on the tree-like structure of knowledge itself. And also recall — for a complete picture — the famous legend about the circumstances under which Descartes invented his coordinate system.
|
||||
|
||||
@ -54,7 +54,7 @@ To understand these rules generally, it's helpful to draw a close analogy with t
|
||||
|
||||
In constructing *p-*adic numbers, something similar is done, but as the base, a prime number is taken — divisible only by itself and 1 (in the German language, such an object is called *Primzahl*, which suggested to Kurt Hensel naming his discovery *p-adischen Zahlen*). Hensel found that if rational numbers, i.e., fractions, are expressed in a specific mathematical way (using modular arithmetic) through the powers of a prime number, a special, entirely full-fledged world of numbers results.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Most importantly, this world provides a convenient approach to well-known complex problems in mathematics. In particular, the *p*-adic framework has proven very useful for clarifying general questions about the solvability of algebraic equations.
|
||||
|
||||
@ -98,7 +98,7 @@ Well, the direct relevance of this entire construction to the mathematics of *p-
|
||||
|
||||
So from the very beginning and up to this day, *p-*adic numbers have been although not the only, but undoubtedly the most important example of ultrametric spaces. Or a system of infinitely nested spheres "whose center is everywhere and the circumference nowhere."
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>Conventional depiction of 3-, 5-, 7-adic numbers (in reality, there are no gaps between circles)</center>
|
||||
|
||||
|
||||
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(52)</center>
|
||||
|
||||
@ -20,23 +20,23 @@ In principle, there are various ways to discuss this " structure of our space" d
|
||||
|
||||
Basically, Heinz Hopf found a way to fill all of space with circles. Generally speaking, for this task, there are simple solutions like this – take a straight line and string onto it concentric circles ad infinitum.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
However, Hopf tackled a more general task – the construction of a mapping of a three-dimensional spherical surface or 3-sphere, located in 4-dimensional space, onto the more familiar 3-dimensional Euclidean space, which is commonly referred to as flat and denoted **R<sup>3</sup>**.
|
||||
|
||||
In a sense, this task is analogous to the problem of how to display the surface of a globe – or 2-sphere – onto the surface of a flat map. It is clear that any form of projection inevitably introduces various distortions to the picture. For this purpose, Hopf applied the known stereographic projection in geography and geometry that preserves angles between lines (this is called conformal transformation), and circles are also translates into circles or straight lines (alternatively, circles of infinite radius).
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
If one develops the same analogy with the globe, i.e., the more familiar 2-sphere, one of the important features of the mapping studied by Hopf is this. When the points of the 3-sphere forming the surface in 4-dimensional space are arranged on such a globe strictly along the line of "latitude," then in Euclidean space **R<sup>3</sup>**, this configuration corresponds to a shape known as a torus of revolution (and in form corresponds to a vortex ring).
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The thickness of the tube of such a torus changes depending on the location of the latitude between the plane and the projection point. As the latitude shifts from the projection point, the torus passes through all intermediate states between two extreme ones. In one extreme, becoming ever thinner, it degenerates into a circle. In the opposite case, the torus swells to such an extent that its "hole" degenerates into a straight line perpendicular to the equatorial plane.
|
||||
|
||||
In other words, Hopf filled all of space **R<sup>3</sup>** with nested tori. But the most important thing here is this. For each point on the globe, located on the latitude line, there is a corresponding circle line on the torus surface. This line captures the "donut hole" and obliquely encircles the tube. Just as a multitude of points fill the entire circumference of latitude, so a collection of such rings, linked with each other, completely covers the surface of the respective torus.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
For historical reasons, such circles on the torus are called Clifford parallels – after an English mathematician who introduced these objects in the 19th century to study the properties of curved spaces. Therefore, this whole construction is sometimes called the Clifford-Hopf fibration. Fibers here are those linked circles that form the surfaces of the tori, and hence – fill the entire volume of space.
|
||||
|
||||
@ -44,7 +44,7 @@ This initial construction gave rise to an extremely fruitful direction in topolo
|
||||
|
||||
By the end of the 1970s, however, it became clear to physicists that the Hopf fibration plays a fundamentally important role in gauge approaches to quantum field theory. It also effectively served as the core of the entire model in Roger Penrose's twistor theory, and later in several other approaches to quantum gravity theory.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Today, the list of possible physical applications for this construction is very long – from magnetic monopoles to the polarization of transverse waves and solid-state mechanics, from the geometric properties of quantum entanglement and the organization of qubits in a quantum computer to the relativistic deformation of the celestial sphere. [o52]
|
||||
|
||||
@ -94,23 +94,23 @@ Initially, it's helpful to consider how such seemingly different configurations
|
||||
|
||||
With the help of mathematical programs and computer graphics, among other things, specialists have shown how a 2-dimensional torus through smooth topological transformations (called homotopy) transforms through compressions, pinches, and stretches into a double-layered Riemann sphere. [o55]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The grid of cells applied to the surface of the torus and twice reproducing the well-known configuration of a soccer ball is, of course, not accidental. Firstly, it allows for a more clear view of the deformation process, demonstrating the topological equivalence of the two distinct structures.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Secondly, as shown by fullerene molecules in nature, such a configuration is optimal in terms of minimizing energy on a spherical surface. Thirdly, most importantly, science today has substantial evidence that this very configuration underlies the structure of the universe — as a network of cells formed by superclusters of galaxies. [i71]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
More precisely, when carefully articulated, the observational data available to science allows for the supposition of a cosmic form known as Poincaré's dodecahedral space. A simplified model of such a configuration is a ball sewn from 12 pieces in the shape of regular pentagons. Or, otherwise, a regular polyhedron-dodecahedron inflated to a sphere. [i72]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Distinct signs of this form of the cosmos were detected by J. Luminet's group in the cosmic microwave background radiation maps from the WMAP satellite [i73]. Polish researchers from Torun University identified on the same map 6 pairs of matching circles, even more definitively indicating the features of a closed-universe space in the shape of a dodecahedron. [i74]
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
To clarify that this significant (but for some reason hushed-up) scientific discovery of the 21st century does not contradict the "classic" form of a soccer ball made out of 12 pentagons and 20 hexagons, one should note that even in the 32-cell variant, there are the same 6 pairs of "circles" as in the dodecahedron. Also, recall the dual topology of the cosmic sphere and the physics of forming convective cells in superfluid liquids. [i75]
|
||||
|
||||
@ -120,7 +120,7 @@ And if on one side of the sphere 12 dodecahedral structure cells form, on the ot
|
||||
|
||||
In the end, when this entire configuration stabilizes to a minimum-energy state, on each side of the sphere—inside and outside—there are identical grids of 32 soccer ball cells, shifted relative to each other by convective processes. These vortex processes effectively "cut off" the energy-costly vertices of the dodecahedron and the icosahedron, overlaying both structures shifted onto each other and ultimately generating a symmetrical, energetically optimal construction.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
If the key role of (topological) vortex effects in the picture of the formation of the cosmic cellular structure has become more or less clear, it is time to remind of the following. All the discussions here are certainly not proofs and, even more so, not the absolute truth.
|
||||
|
||||
@ -132,19 +132,19 @@ Continuing in the same direction, it is time to more thoroughly examine why the
|
||||
|
||||
As an elementary example illustrating what comprises a trivial fibration, the form of a cylinder is typically referenced, formed from segments stemming from multiple points on a circle. The surface of such a cylinder is called a circle fibration, with its constituent segments dubbed fibers.
|
||||
|
||||
<center></center>
|
||||
 and non-trivial fiber bundle")
|
||||
|
||||
Accordingly, a fibration is called nontrivial if the surface formed by the fibers demonstrates one-sidedness rather than being ordinary. The simplest example of such a surface — a nontrivial fibration — is the Möbius strip.
|
||||
|
||||
To make it clearer how in the nontrivial Hopf fibration, where the fibers are circles, a crucial structure like the Möbius strip is present, it's helpful to introduce two seemingly different figures that are, in fact, topologically equivalent. One in the form of a ladder graph represents the traditional essence of the Möbius strip as a one-sided surface, while the other, employing the rubbery properties of topology, elongates the same graph into a circle, with opposite points connected by segment-fibers.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The extent to which the nontrivial topology of a Möbius strip can be significant from the perspective of physics was recently beautifully demonstrated once more by a group of Chinese researchers from Beijing's Institute of Theoretical Physics [o56]. In 2009, they published a theoretical paper on the electronic properties of a sheet made of a new material, graphene, and taking the shape of a Möbius strip.
|
||||
|
||||
In this research, calculations demonstrated that a graphene Möbius strip behaves as a "topological insulator with a robust metallic surface" [i76]. That is, electron movements occur losslessly along the edge of the strip, while the rest (bulk) of the strip doesn't conduct electricity, showcasing insulating properties. In other words, the topology of the shape engenders the material's unusual properties.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Three years later, in May 2012, theoretical work from the Institute for Nuclear Theory in Seattle, USA, showed that if the known physical properties of a topological insulator are assumed for the space-time of the entire universe, then it is possible to discern a completely natural topological mechanism that generates precisely three generations of fermion particles. [o57]
|
||||
|
||||
@ -156,7 +156,7 @@ To spectacularly enhance the same "layered" theme, one can revisit the smooth ho
|
||||
|
||||
One of transformations shown by Trott through animated clips illustrates the morphing process between the already known two-layered soccer ball and the trefoil knot — another noteworthy form rich in its topological properties.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center></center>
|
||||
|
||||
@ -182,35 +182,31 @@ Among the key achievements of the holographic approach in modern theoretical phy
|
||||
|
||||
To make the direct connection between AdS/CFT and Hopf fibration more clear and illustrative, it is useful to describe two different but equivalent approaches to filling the volume with curved surfaces. One of these methods, (a), is already familiar to us and represents Clifford parallels in the form of circles forming tori. The second method, (b), linearizes the first, so that Clifford parallels indeed become line segments, but at the same time form a curved "ruled surface" or hyperboloid of revolution with negative curvature. The boundary of such a surface is a circle or 1-sphere.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Based on these images, showing the connections with AdS/CFT becomes simpler. Because the outer part of a torus with positive curvature can be likened to the world of the spherical boundary system of CFT (here dimension 2D). And the inner space of the "hole," bounded by a hyperboloid of negative curvature, can be considered as the world of AdS (dimension 3D, respectively).
|
||||
|
||||
In this modeling approach, AdS space-time looks like a stack of flat (2D) circles, each having a hyperbolic geometry of space, and all stacked on top of one another along the vertical time axis (forming 3D).
|
||||
|
||||
<center></center>
|
||||
|
||||
<center>Left: Projection of hyperbolic space onto a plane. Each fish is actually the same size, and the boundary circle is infinitely far from the center of the disk. The compression of the fish sizes is done to fit an infinite space within a circle of finite size. This is a visual effect of strong spatial curvature. Center and right: Physics in such a space-time (“stack of disks”) is quite specific. Both a ball and a beam of light, launched from the center of the disk, return back in the same amount of time (with the distinction that the light manages to reach the edge of space). For details, see [o58]</center>
|
||||
|
||||
<center></center>
|
||||
|
||||
<center></center>
|
||||
 is quite specific. Both a ball and a beam of light, launched from the center of the disk, return back in the same amount of time (with the distinction that the light manages to reach the edge of space). For details, see [o58]")
|
||||
|
||||
If one makes a cross-section of the torus at any given moment in time, then every circle in the AdS world corresponds to a latitude circle on the outer shell — a snapshot of “our” CFT world. A 1D world that, along the same time axis, moves from the past (the bottom of the torus) to the future (the top of the torus).
|
||||
|
||||

|
||||
|
||||
Since the "AdS world" geometrically resides in the "hole" of the torus, and every circle in the Hopf fibration forming the surface of the torus necessarily contains this "hole" inside, an intriguing possibility is visible for the point inhabitants of the "CFT world" living at the latitude. If considering the inclined circle of the Hopf fiber as their "memory," i.e., the basis of consciousness, the space inside that circle falling within the "hole" of the torus can be thought of as the 2-dimensional "hologram of consciousness." Moreover, due to the geometric features of the inclined section, this hologram allows the inhabitants of the "CFT world" to travel within their consciousness both in space and time.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
As everyone knows, in a similar way — by the "power of thought" — people in our world can travel through space-time in their dreams, reveries, and in memories of near-death experience linked to staying in the other world of spirits and souls of the deceased. In other words, there are reasons to name this space — geometrically inseparably connected with ours — as the space of the other world.
|
||||
|
||||
A significant point in AdS/CFT considerations is that the CFT physics on the boundary-shell, while generally similar to the physics of our world, lacks gravity. On the contrary, the physics of the 5-dimensional AdS, although this world is otherwise completely unlike ours, includes gravity naturally.
|
||||
|
||||
To understand how this apparent, at first glance, discrepancy with the physics of the real world is overcome, it is useful to recall again the 2-brane Randall-Sundrum model, which requires 5 dimensions (see [4.4](https://kniganews.org/2013/01/01/beyond-clouds-44/)). And about the fact that the mysterious world of the "gravity brane" in their model can be much more naturally explained through the world of the membrane as a closed one-sided surface of the Möbius strip type. Where the second half of all the particles of our world is concentrated in stars. Or, in other words, in those regions of space whose geometry is strongly deformed by gravity effects.
|
||||
To understand how this apparent, at first glance, discrepancy with the physics of the real world is overcome, it is useful to recall again the 2-brane Randall-Sundrum model, which requires 5 dimensions (see [4.4](/tbc/44/)). And about the fact that the mysterious world of the "gravity brane" in their model can be much more naturally explained through the world of the membrane as a closed one-sided surface of the Möbius strip type. Where the second half of all the particles of our world is concentrated in stars. Or, in other words, in those regions of space whose geometry is strongly deformed by gravity effects.
|
||||
|
||||
It is also appropriate here to remind and add such an essential nuance to this picture. Due to the constant flipping of particles from one side of the membrane to the other, we — as observers — find ourselves inside and then outside the surface of the sphere all the time. In such conditions, the natural averaging of all our observations concerning the curvature of space is that the geometry of the universe everywhere appears flat — like a sheet of paper on a table…
|
||||
|
||||
Finally, another notable consequence of this construction, as previously demonstrated (see [4.3](https://kniganews.org/2012/12/30/beyond-clouds-43/)), is the effect of topological charge inversion with each flip of a particle from one side of the membrane to the other. If considering this process in terms of Dirac's magnetic monopole, it is not difficult to see that here precisely lies the geometric answer to the mysterious elusiveness in nature of the so desired object for theorists.
|
||||
Finally, another notable consequence of this construction, as previously demonstrated (see [4.3](/tbc/43/)), is the effect of topological charge inversion with each flip of a particle from one side of the membrane to the other. If considering this process in terms of Dirac's magnetic monopole, it is not difficult to see that here precisely lies the geometric answer to the mysterious elusiveness in nature of the so desired object for theorists.
|
||||
|
||||
In some sense, the search for Dirac's monopole is roughly the same as trying to see the whole particle, which on one side of the membrane is a proton, and on the other, an electron.
|
||||
|
||||
|
||||
222
data/tzo/7.md
222
data/tzo/7.md
@ -1,4 +1,4 @@
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(58)</center>
|
||||
|
||||
@ -24,7 +24,7 @@ Particularly noteworthy in this picture are the following points: First, in anci
|
||||
|
||||
In particular, in Plato's work "The Republic," the functioning of the world order is explained as the result of the action of the cosmic spindle of Ananke. In the image of the goddess Ananke, we should remind, in Greek mythology, represents Necessity or Inevitability.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Ananke was the mother of the three Moirai — executors of human fates. She herself, according to Plato, governs the entire spinning of the fabric of the cosmos. Between Ananke's knees rotates the spindle, whose axis is the axis of the universe. And the daughters-Moirai — as best as they can — assist this universal rotation…
|
||||
|
||||
@ -56,21 +56,19 @@ Far more significant for the physic-mathematical science are the 12 indicated su
|
||||
|
||||
Why and to what extent this is important for the modern scientific worldview will become clearer as we delve into the mythological ideas of the ancients, the religious philosophy of the East, and the revelations of mystics of the West.
|
||||
|
||||
<center></center>
|
||||
|
||||
.
|
||||

|
||||
|
||||
<center>(59)</center>
|
||||
|
||||
First and foremost, to vividly illustrate how it can generally occur — when people have a multitude of such knowledge which they themselves are unable to explain or comprehend — it suffices to recall "Dream # 59," dreamt by the outstanding physicist Wolfgang Pauli. [o61]
|
||||
|
||||
Under the number 59, it should be clarified, this remarkable dream appears in the works of Carl G. Jung, who tried — albeit entirely unsuccessfully — to analyze and explain it from the scientific positions of analytical psychology. Pauli himself called it "The Great Vision of the World's Clocks," which evoked a very profound and lasting sensation of "the most exalted cosmic harmony," comparable in its effect on the psyche to religious enlightenment. [i80]
|
||||
Under the number 59, it should be clarified, this remarkable dream appears in the works of Carl G. Jung, who tried — albeit entirely unsuccessfully — to analyze and explain it from the scientific positions of analytical psychology. Pauli himself called it "The Great Vision of the World Clock," which evoked a very profound and lasting sensation of "the most exalted cosmic harmony," comparable in its effect on the psyche to religious enlightenment. [i80]
|
||||
|
||||
That is, Pauli understood quite definitely that from the depths of his own consciousness he received through this image some extremely important information about the workings of the universe. The scientist remembered the picture perfectly and in details, but — despite his undeniable talents in mathematics and physics — was unable to comprehend what exactly this picture meant.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The compact format of this book is not very suitable for detailed decoding of the entire construction of the "World's Clocks," however, to explain the key parameters of the structure — two mutually perpendicular dials with 32 sectors— there is quite enough space. But for the result of the decryption to appear as a natural and convincing explanation, it's necessary to recall some facts from the history of clocks.
|
||||
The compact format of this book is not very suitable for detailed decoding of the entire construction of the "World Clock," however, to explain the key parameters of the structure — two mutually perpendicular dials with 32 sectors— there is quite enough space. But for the result of the decryption to appear as a natural and convincing explanation, it's necessary to recall some facts from the history of clocks.
|
||||
|
||||
The division of the daily cycle into 12 parts began long before the appearance of mechanical clocks with hands and round dials. The number 12 — for reasons unclear to science — astronomers of deep antiquity in different parts of the world somehow chose for dividing the annual cycle and segmenting the sky with zodiac constellations.
|
||||
|
||||
@ -98,7 +96,7 @@ An unquestionably important point is that here we have an absolutely precise coi
|
||||
|
||||
Equally significant seems another — hitherto unmentioned — feature of the "clocks of the world," referring to the process of overall evolution of the cosmos and humankind. In Pauli's dream, this is conveyed as a change of color in the outer ring of the dial: "A ring borders the circle, which was once dark, but now is golden."
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center></center>
|
||||
|
||||
@ -134,7 +132,7 @@ Regarding existence on the "divine" level, in this phase, according to Empedocle
|
||||
|
||||
Regrettably, the extraordinarily distinctive teaching of Empedocles did not take root in ancient Greek culture. After the philosopher's death, no disciples remained capable of continuing his work, nor was there a school to develop and spread Empedoclean ideas.
|
||||
|
||||
<center>* * *</center>
|
||||
<center># # #</center>
|
||||
|
||||
However, it is worth noting that in the very same historical period when the extraordinary thinker Empedocles was living and teaching in the Mediterranean, another sage was teaching a new perspective on the world in a completely different region of the planet, on the Indian subcontinent, known by the names Siddhartha Gautama, Shakyamuni, or simply Buddha.
|
||||
|
||||
@ -158,13 +156,13 @@ However, for all living beings, who in the process of reincarnation receive —
|
||||
|
||||
For the Buddhist universe is arranged such that only humans have the capability to fully control their consciousness, achieve enlightenment, and, if desired, leave the realms of rebirth entirely, becoming a Buddha and entering nirvana—the highest level of existence in a state of complete freedom and blissful union with the void of unity. And if desired, one can live on, but now as enlightened beings — bodhisattvas, saints helping all others to attain enlightenment.
|
||||
|
||||
<center>* * *</center>
|
||||
<center># # #</center>
|
||||
|
||||
If we attempt to translate the Buddhist worldview into the language of contemporary physics-mathematics, one of the first — evidently useful for this matter — constructs appears to be the Randall-Sundrum model or RS (see TBC section 4.4, chapter 29).
|
||||
If we attempt to translate the Buddhist worldview into the language of contemporary physics-mathematics, one of the first — evidently useful for this matter — constructs appears to be the Randall-Sundrum model or RS (see [TBC section 4.4, chapter 29](/tbc/44/#chapter29)).
|
||||
|
||||
Besides offering a beautiful explanation for the striking difference in the forces of electromagnetism and gravity through the use of two branes, the "RS model" also provides mathematical justification for a multi-layer structure of multiverse space, located between two boundary membranes.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center></center>
|
||||
|
||||
@ -178,7 +176,7 @@ It's understood that animals, whose bodies consist of the same basic elements as
|
||||
|
||||
As for the inhabitants of all other Buddhist worlds (devas and asuras, pretas and hellish beings), they, as entities not registered in our world by physical observations, naturally end up as constant inhabitants of other so-called "subtle" layers of the universe.
|
||||
|
||||
<center>* * *</center>
|
||||
<center># # #</center>
|
||||
|
||||
One idea of Buddhists deserves special consideration, namely that human consciousness — with its vast range of layer coverage — in its different states of emotional and mental activity, exists at different levels of the multi-tiered universe.
|
||||
|
||||
@ -188,11 +186,11 @@ Intuitively, it's probably not difficult to comprehend that by combining these t
|
||||
|
||||
To make the general dynamics of the development of this geometric structure in time and space more comprehensible, it's useful to recall two significantly different ways through which the space is filled with circles: (a) a trivial way and (b) a nontrivial Hopf fibration.
|
||||
|
||||
<center>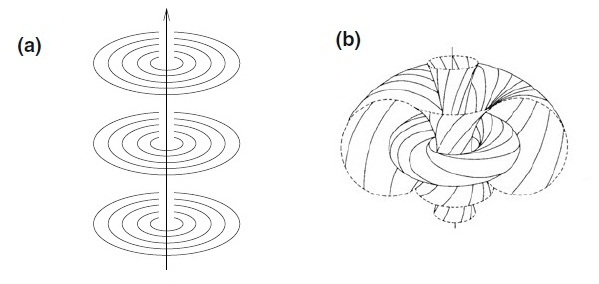</center>
|
||||

|
||||
|
||||
By a non-accidental, naturally occurring coincidence, these two images in the simplified (a) and more intricate — but also more adequate — view (b) reflect the process of the evolution of the world and humanity as envisioned by ancient Buddhists and Empedocles. To put it differently, we can say that these are two different projections that display a unified multi-dimensional structure as an easier-to-understand three-dimensional image for us.
|
||||
|
||||
To explain image (a), one could refer to the "Abhidharma Encyclopedia," the most authoritative compilation of cosmological information in Buddhism, compiled in the 5th century AD. According to this source, in the Buddhist model of the world, the foundation of the universe is a dense vortex of air. Above this vortex is a very thick layer of water, and on top of it — the uppermost layer of "our" dense world, once made of iron, now of gold. (For comparison—in Pauli's world clocks, the outer rim of the dial was dark, and now it is golden.)
|
||||
To explain image (a), one could refer to the "Abhidharma Encyclopedia," the most authoritative compilation of cosmological information in Buddhism, compiled in the 5th century AD. According to this source, in the Buddhist model of the world, the foundation of the universe is a dense vortex of air. Above this vortex is a very thick layer of water, and on top of it — the uppermost layer of "our" dense world, once made of iron, now of gold. (For comparison—in Pauli's world clock, the outer rim of the dial was dark, and now it is golden.)
|
||||
|
||||
It is hardly reasonable to make hasty judgments about the "non-physical" nature of this strange worldview. For it is easy to see that contemporary astrophysics reliably establishes precisely such a path of evolution for the matter of the universe: from the lightest elements, hydrogen and helium (air), further to the heavier oxygen (i.e., to water, as its compound with hydrogen), and then to the synthesis of heavier elements like iron and gold…
|
||||
|
||||
@ -206,11 +204,11 @@ But as all beings go through purification in reincarnation processes on differen
|
||||
|
||||
As Empedocles stated about this process, driven by the power of Love, all living beings strive for unity in "venerable harmony." In the Buddhist universe's cylindrical structure, however, a place for nirvana is not very visible and is vaguely named as "the other shore." Yet, if one relies on Empedocles' idea of Sphairos and imagines a multi-dimensional sphere in a modern fashion, in the form of a Hopf fibration, the picture of the future for humanity and the world becomes much clearer.
|
||||
|
||||
<center>* * *</center>
|
||||
<center># # #</center>
|
||||
|
||||
From the above discussions, it can be understood that the structure of subtle human bodies and the multi-dimensional construction of the universe's space-time is convenient (and beneficial) to view collectively as a unified whole. Additionally, when transitioning to representing both in the form of a set of nested tori, it is again convenient to interpret image (b) in application to different vertical axes—time and frequency vibrations.
|
||||
|
||||
Previously (in section TBC 6.2) it was already demonstrated that on the torus surface, the outer horizontal circle, when moving along the time axis, well conveys the evolution of the space of the observable universe: emergence from the vortex funnel at the base, expansion to maximum size, and then contraction in the area of the top torus funnel.
|
||||
Previously (in [TBC section 6.2](/tbc/62/)) it was already demonstrated that on the torus surface, the outer horizontal circle, when moving along the time axis, well conveys the evolution of the space of the observable universe: emergence from the vortex funnel at the base, expansion to maximum size, and then contraction in the area of the top torus funnel.
|
||||
|
||||
It was also mentioned that every material object, including a human, on this universal circle is represented by a point. And the trajectory (worldline) of each such point in space-time on the torus surface looks like an oblique circle. Or — in mathematical terminology — a fiber in the Hopf fibration.
|
||||
|
||||
@ -224,17 +222,17 @@ Delving further into this mechanic, it's not difficult to figure out how bad kar
|
||||
|
||||
Here, however, it's much more interesting to examine not the mechanics of reincarnations and karma cleansing in the Buddhist worldview (as thoroughly described in countless books), but the geometric, so to speak, aspects of human evolution towards the highest level of consciousness, otherwise known as "enlightenment" or "reaching the other shore."
|
||||
|
||||
<center>* * *</center>
|
||||
<center># # #</center>
|
||||
|
||||
One of the most remarkable features of the Hopf fibration is that important details of this specific geometric construction were well-known to people earlier, in various contexts: mathematically, philosophically-mystically, and religiously-practically.
|
||||
|
||||
Speaking specifically about mathematics, the inclined circles forming the torus surface were historically discovered and described by the French astronomer Yvon Villarceau back in 1848. That is, almost a century before Hopf's discovery of topological fibrations, Villarceau showed that when a torus is bisected by a plane touching its surface twice, a characteristic figure is formed, consisting of two circles whose centers lie on each other's perimeters.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
A direct outcome derived from the discovery of Villarceau's circles is this fact. Through any randomly chosen point on the torus surface, it turns out that four different circles always pass. Two are obvious and relate to the torus as a rotating figure's circular generatrices. Thus, one circle lies in a plane parallel to the equatorial plane of the torus, and the other — perpendicular to it. As for the other two, less-obvious circles, these are two "oblique" Villarceau circles, generally lying in different planes corresponding to different bisecting planes.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
For the constructed correspondences picture, these 4 circles intrinsic to each point on the torus matter for the following reasons. The first two circles — horizontal and vertical —indicate the universe's closure on space and time axes. The skew circle of Villarceau, clearly, signifies the "world line" trajectory of any object in the universe's evolution. But the fact that TWO such skew circles actually pass through any point — that fact requires particular attention and consideration.
|
||||
|
||||
@ -246,7 +244,7 @@ Yet, geometry allows for situations where both circles end up in one plane or be
|
||||
|
||||
Naturally, it's no accident that such a configuration was known in the so-called "sacred geometry" of various Eastern and Western cultures for many centuries and even millennia before Yvon Villarceau's discovery. This figure appears under different names but is most frequently called Vesica Piscis in mystical literature of the European tradition of the last 3-4 centuries, which translates as "fish bladder" from Latin.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
For a clearer understanding of the natural interpretation of this "sacred" geometry from the perspective of a person's psychological self-realization, two points ought to be emphasized. Firstly, the well-known formula that "nature is a sphere whose center is everywhere and circumference nowhere."
|
||||
|
||||
@ -260,36 +258,34 @@ Such profound ideas of universal unity, in fact, can be discovered in the simple
|
||||
|
||||
The essence of these ideas, however, people have always been able to grasp without any science. Undoubtedly curious and worthy of mention is the fact that the central element of the Vesica Piscis, having a special name Mandorla (or "almond" in Italian), was quite popular in the religious visual art of medieval Europe.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The characteristic form of the Mandorla was often used to depict a glowing (or conversely dark) halo around Christian saints, the Virgin Mary, and her son Jesus. What exactly the ancient masters intended in this image is hard to say. But it is impossible to deny that for this characteristic form, at least three comparisons are valid.
|
||||
|
||||
Firstly, it is the form of the cosmic spindle of Ananke, located "between her knees." Secondly, it is the traditionally accepted form for depicting the female reproductive organ. And thirdly, this form is an adequate representation for the contours of the "holographic AdS world," formed by the universal collective consciousness in the "black hole" of the torus universe (for details of this interpretation, see TBC part 6.2, chapter 56).
|
||||
Firstly, it is the form of the cosmic spindle of Ananke, located "between her knees." Secondly, it is the traditionally accepted form for depicting the female reproductive organ. And thirdly, this form is an adequate representation for the contours of the "holographic AdS world," formed by the universal collective consciousness in the "black hole" of the torus universe (for details of this interpretation, [see TBC section 6.2, chapter 56](/tbc/62/#chapter56)).
|
||||
|
||||
Moreover, to further emphasize the importance of the geometric properties of the universe demonstrated by the Hopf fibration, the following feature of this structure should be mentioned. When in the late 1980s to early 1990s, graphic software and personal computers began to be used for the rigorous mathematical representation and analysis of this object, a remarkable fact was discovered. [o63]
|
||||
|
||||
It turned out that **each oblique circle**, forming the surface of the torus in the Hopf fibration, is strictly **linked once with all other circles** of the structure. Moreover, each of the rings is linked not only with the rings of "its" torus but also with each ring of all other tori of the fibration.
|
||||
It turned out that **each oblique circle**, forming the surface of the torus in the Hopf fibration, is strictly **linked once with all other circles**
|
||||
of the structure. Moreover, each of the rings is linked not only with the rings of "its" torus but also with each ring of all other tori of the fibration.
|
||||
|
||||
In other words, concerning the model of the universe, the life line and consciousness of literally every being in nature are inextricably linked with the soul of absolutely all other inhabitants of the universe — living in all its frequency layers.
|
||||
|
||||
A stronger image for the universal unity of the world is probably impossible to conceive.
|
||||
|
||||
<center></center>
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>(61)</center>
|
||||
|
||||
Another very important — or archetypal — image that has consistently persisted in human culture from ancient times to the present is the symbol of the butterfly.
|
||||
|
||||

|
||||
|
||||
A rather unexpected and original illustration demonstrating the truly universal character of this archetype (ranging from the mysteries of the universe to human evolution) can be found in the following fragment from the poems of Vladimir Nabokov:
|
||||
|
||||
> No, life is no quivering quandary!
|
||||
|
||||
> Here under the moon things are bright and dewy.
|
||||
|
||||
> We are the caterpillars of angels; and sweet
|
||||
|
||||
> No, life is no quivering quandary!<br>
|
||||
> Here under the moon things are bright and dewy.<br>
|
||||
> We are the caterpillars of angels; and sweet<br>
|
||||
> It is to eat from the edge into the tender leaf…
|
||||
|
||||
For Nabokov's work — the only great Russian writer who wrote equally remarkable works in both his native language and English — the image of the butterfly, as many know, was far from accidental.
|
||||
@ -326,9 +322,9 @@ How close this concept might have been to both the writer and the physicist is e
|
||||
|
||||
As a visual illustration of this idea applied to the field of physics, it would be appropriate, perhaps, to provide the following comparison picture, presupposing for the viewers not only the ability to analyze facts but also at least a minimum of imagination.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
In these pictures, one can see three essentially simple images reflecting fundamentally important ideas for modern physics. (a) The construct of a [<u>graviton as a pair of photons</u>](https://kniganews.org/2013/01/01/beyond-clouds-44/), providing unity to a world split into two identical parts. (b) A strange attractor, as a graph of the "bifurcated" behavior of a nonlinear dynamic system on the brink of order and chaos. (c) A cross-section of a torus as Villarceau circles, as a simplest representation of the holographic idea of [<u>AdS/CFT correspondence</u>](https://kniganews.org/2013/05/10/beyond-clouds-62/https://kniganews.org/2013/05/10/beyond-clouds-62/) and the inseparable unity of two substantially different worlds, forming a whole.
|
||||
In these pictures, one can see three essentially simple images reflecting fundamentally important ideas for modern physics. (a) The construct of a [graviton as a pair of photons](/tbc/44/), providing unity to a world split into two identical parts. (b) A strange attractor, as a graph of the "bifurcated" behavior of a nonlinear dynamic system on the brink of order and chaos. (c) A cross-section of a torus as Villarceau circles, as a simplest representation of the holographic idea of [AdS/CFT correspondence](/tbc/62/) and the inseparable unity of two substantially different worlds, forming a whole.
|
||||
|
||||
When all these pictures are selected and displayed in a row like this, any particularly attentive person can probably discern the same image-archetype behind each of them. The second — most known — of the pictures, incidentally, is commonly referred to by the name "Lorenz's butterfly."
|
||||
|
||||
@ -405,9 +401,9 @@ In 1933, in one of his last books, "My Philosophy," Oliver Lodge summarized the
|
||||
To convey how Lodge's scientific colleagues viewed these studies, it is appropriate to include a quote from a 1935 article [o68] by the outstanding Soviet physicist Lev Landau:
|
||||
|
||||
> I had occasion to ask average English laypeople: who is the best physicist in England? The responses mentioned not the world-famous names of Rutherford and Dirac, but to my surprise, I learned that the greatest physicist in England is Sir Oliver Lodge.
|
||||
|
||||
>
|
||||
> Very few physicists outside of England have heard this name. It is difficult to establish that about 50 years ago Oliver Lodge really engaged in physics, but did not particularly distinguish himself. The secret of such popularity is that although Oliver Lodge knows little about physics, he successfully summons spirits and even managed to photograph them.
|
||||
|
||||
>
|
||||
> The fact that this "genius" physicist, as can be read in any English newspaper, simultaneously engages in spiritualism should serve as proof of the absence of contradiction between physics and such nonsense as the afterlife…
|
||||
|
||||
For a more objective perception of this tirade, it's worth noting that Lev Landau, who wrote these words, was 27 years old at the time, while Lodge was 84. But even if we attribute the young man's outright rudeness towards an elderly and honorable person to the specifics of Soviet life, we must nonetheless acknowledge the obvious. Landau's position is the general, absolutely dominant point of view in current global science on the fundamentally important, yet essentially unresolved issue of understanding the nature of our consciousness.
|
||||
@ -444,9 +440,9 @@ And then there are the fresh impressions of a person completely unaccustomed to
|
||||
|
||||
These are the words Alexander uses to convey the effect of his complete immersion into this hologram:
|
||||
|
||||
It seemed that you could not look at or listen to anything in this world without becoming a part of it — without joining with it in some mysterious way.
|
||||
|
||||
From my present perspective, I would suggest that you couldn’t look at anything in that world at all, for the word at itself implies a separation that did not exist there. Everything was distinct, yet everything was also a part of everything else, like the rich and intermingled designs on a Persian carpet… or a butterfly’s wing.
|
||||
> It seemed that you could not look at or listen to anything in this world without becoming a part of it — without joining with it in some mysterious way.
|
||||
>
|
||||
> From my present perspective, I would suggest that you couldn’t look at anything in that world at all, for the word at itself implies a separation that did not exist there. Everything was distinct, yet everything was also a part of everything else, like the rich and intermingled designs on a Persian carpet… or a butterfly’s wing.
|
||||
|
||||
As the doctor's mind conjures the image of a butterfly, a guide appears beside him. Initially, in the form of a young and attractive woman: high cheekbones, blue eyes, light brown braids, simple but vividly colored peasant clothing. Meanwhile, the butterfly image in the picture intensifies:
|
||||
|
||||
@ -462,15 +458,15 @@ Let us simply note this intriguing image for remembering and later analysis (for
|
||||
|
||||
We must remind of one essential nuance here. As explained by Alexander, this near-death journey into another reality was only undertaken by a part of his consciousness. That "upper" part, which was able to remember everything in detail upon return, was completely separate from the main attributes of his personality "here" — like name, age, profession, place of residence, and so on. Understanding this helps better interpret the subsequent communications:
|
||||
|
||||
Although I still had little language function, at least as we think of it on earth, I began wordlessly putting questions to this wind: Where is this place? Who am I? Why am I here?
|
||||
|
||||
Each time I silently posed one of these questions, the answer came instantly in an explosion of light, color, love, and beauty that blew through me like a crashing wave.
|
||||
|
||||
What was important about these bursts was that they didn’t simply silence my questions by overwhelming them. They answered them, but in a way that bypassed language.
|
||||
|
||||
Thoughts entered me directly. But it wasn’t thought like we experience on earth. It wasn’t vague, immaterial, or abstract.
|
||||
|
||||
These thoughts were solid and immediate — hotter than fire and wetter than water — and as I received them I was able to instantly and effortlessly understand concepts that would have taken me years to fully grasp in my earthly life…
|
||||
> Although I still had little language function, at least as we think of it on earth, I began wordlessly putting questions to this wind: Where is this place? Who am I? Why am I here?
|
||||
>
|
||||
> Each time I silently posed one of these questions, the answer came instantly in an explosion of light, color, love, and beauty that blew through me like a crashing wave.
|
||||
>
|
||||
> What was important about these bursts was that they didn’t simply silence my questions by overwhelming them. They answered them, but in a way that bypassed language.
|
||||
>
|
||||
> Thoughts entered me directly. But it wasn’t thought like we experience on earth. It wasn’t vague, immaterial, or abstract.
|
||||
>
|
||||
> These thoughts were solid and immediate — hotter than fire and wetter than water — and as I received them I was able to instantly and effortlessly understand concepts that would have taken me years to fully grasp in my earthly life…
|
||||
|
||||
As is often the case with those who return 'from there' with inspired and transformed consciousness, Alexander finds it's not possible to convey those grand ideas and concepts he naturally understood 'there' using familiar human notions 'here'. The doctor realizes that we currently lack the right words for this. So he describes his experiences as best he can. In particular, about the following crucial episode of 'grasping the void':
|
||||
|
||||
@ -478,13 +474,13 @@ As is often the case with those who return 'from there' with inspired and transf
|
||||
|
||||
And to make such an unusual state absolutely comfortable for a person, he receives both light and a beautiful loving guide — all in one:
|
||||
|
||||
Pitch black as it was, it was also brimming over with light: a light that seemed to come from a brilliant orb that I now sensed near me.
|
||||
|
||||
In some manner I couldn’t completely comprehend but was sure of nonetheless, the Orb was a kind of “interpreter” between me and this extraordinary presence surrounding me.
|
||||
|
||||
It was as if I were being born into a larger world, and the universe itself was like a giant cosmic womb, and the Orb (who remained in some way connected to the Girl on the Butterfly Wing, who in fact was she) was guiding me through this process.
|
||||
|
||||
That was it, exactly: an inky darkness that was also full to brimming with light…
|
||||
> Pitch black as it was, it was also brimming over with light: a light that seemed to come from a brilliant orb that I now sensed near me.
|
||||
>
|
||||
> In some manner I couldn’t completely comprehend but was sure of nonetheless, the Orb was a kind of “interpreter” between me and this extraordinary presence surrounding me.
|
||||
>
|
||||
> It was as if I were being born into a larger world, and the universe itself was like a giant cosmic womb, and the Orb (who remained in some way connected to the Girl on the Butterfly Wing, who in fact was she) was guiding me through this process.
|
||||
>
|
||||
> That was it, exactly: an inky darkness that was also full to brimming with light…
|
||||
|
||||
At this intriguing point, the story of Dr. Alexander's journey to the afterlife should perhaps conclude — redirecting all interested to the author's book. And to the hundreds of volumes of similar literature with recollections from various people who have had similar experiences under different circumstances or in different eras.
|
||||
|
||||
@ -536,7 +532,7 @@ As scientists themselves explain this heightened interest, butterfly wings — n
|
||||
|
||||
The specificity of the structure of butterfly wings is such that there is an array formed by light-scattering elements in a regular structure. Thanks to such a regular grid-like nanostructure, a butterfly wing always reflects approximately the same light wave regardless of the angle at which the light falls.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Using scientific terminology, such butterfly wings demonstrate the characteristics of so-called "structural coloration," not the usual "chemical" kind. Much more familiar to everyone, chemical coloration — or the intrinsic color of a specific chemical substance — is explained as the scattering of light in one range of wavelengths and the absorption of waves from other parts of the spectrum. All dyes used have precisely this kind of innate chemical color.
|
||||
|
||||
@ -564,19 +560,17 @@ The idea of natural intelligence turns out to be inextricably linked with the id
|
||||
|
||||
In the collective consciousness of humanity, for conveying and comprehending this idea, the corresponding archetypical symbol has long been developed — a depiction of birds sitting on the branches of the tree of life. But these are not just any birds…
|
||||
|
||||
<center></center>
|
||||
|
||||
<center></center>
|
||||
|
||||
<center>(62)</center>
|
||||
|
||||

|
||||
|
||||
In the memorable dream of Wolfgang Pauli, known as the "Great Vision of the World Clock" [i82], there is one important detail which, for some reasons, has not been mentioned much here before.
|
||||
|
||||
The previously omitted element is the "large black bird" that supports all that intricate construction, which simultaneously powerfully inspired and greatly puzzled the dreamer. Moreover, the intricate clock mechanism remained an unfathomed mystery not only for Pauli himself but also for his much more experienced in such matters friend, Carl Gustav Jung.
|
||||
|
||||
One fragment of the dream was not mentioned for the reason that Jung had absolutely no problems with the interpretation of this particular element – the symbol of the bird.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
Throughout all known human history, the image of a winged bird symbolized spirit, spirituality, supernatural support from otherworldly forces, or simply freedom of mind, flight of thought, and fantasy.
|
||||
|
||||
@ -586,17 +580,17 @@ Although soul-birds with human heads are found in many other cultures, the art o
|
||||
|
||||
In the system of quite intricate notions of the ancient Egyptians about the structure of the world and man, one of the most complex constructs represented the human soul. Like a complex of many nested components with different functionalities – something like a matryoshka doll, animated by a higher mind.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
To delve into the details of this intriguing construct here is clearly not the place, but it is absolutely necessary to emphasize two most important components of the Egyptian soul, in the aggregate unity ensuring its immortal life forever. One part is called Ba, the second Akh, and both are depicted as birds.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The Ba, as a part of the soul, closer to the affairs of the Egyptian’s life, was interpreted as the center of one’s human personality. It was depicted as a bird with a human head and left the physical body after death, in the hope of reuniting with the Akh.
|
||||
|
||||
As for Akh, this highest part of the soul was interpreted as a shining "pure mind" or a personal divine essence that lives by itself and fills every life with meaning. The name of the essence, "Akh," originated from the concept of "sparkling," "shining," "glowing."
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
A Ba that had lived righteously could happily reunite with the cosmic wisdom of the Akh, which was depicted as “just a bird” — an ibis. However, such an end to life was, as far as one can judge, always considered an extremely rare event. As for the souls of ordinary people, after leaving the body and passing the “judgment of the gods,” they would settle across various levels of the afterlife, the Duat, which was described in great detail in the sacred texts of the Egyptians.
|
||||
|
||||
@ -604,7 +598,7 @@ For physico-mathematical analysis of this construct, the following point is part
|
||||
|
||||
That is, the soul of an Egyptian deity contains "many Bas." In the context of the holographic structure of the universe, this is a significant nuance.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
For a logical continuation and development of this theme – "about birds and holography" as aspects of the world's soul structure – it is now convenient to turn to the parables of Sufism, the mystical direction in Muslim philosophy.
|
||||
|
||||
@ -622,9 +616,9 @@ But regardless of this, the birds manage to come to an agreement and set off on
|
||||
|
||||
In the end, finally, thirty of the most persistent reach Mount Qaf, where Simurgh resides. Finally, they see their king in person. And here is where the birds suddenly grasp that they themselves are Simurgh. Each individually and all together…
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
To more clearly explain this very subtle but critically important moment of mystical enlightenment – the comprehension of complete identity between part and whole – it is now convenient to turn to the sacred texts and philosophy of Hinduism. Naturally, in the context of birds as symbols of the soul.
|
||||
|
||||
@ -642,7 +636,7 @@ The word Jiva comes from the Sanskrit root "jiv" – to breathe. In the related
|
||||
|
||||
The word Atman is used to denote another, higher or "cosmic" aspect of the human's immortal soul. This eternal spiritual essence, the highest self, is realized by people after "enlightenment" or Awakening, when they recognize themselves and their existence as "Atma," often translated as "I am not this, I am THAT." With the realization comes the understanding that Atman is identical to the multitude of higher "selves" of all living beings in the world – that is, Brahman…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
In the philosophy of Buddhism, which grew out of the roots of traditional Indian religion, the idea of a "cosmic" Atman, soaring above good and evil, was rejected for some reasons to be replaced by a more grounded concept of the "nature of Buddha," potentially inherent in every person's consciousness.
|
||||
|
||||
@ -668,7 +662,7 @@ As often happens, a mysterious secret added a special allure to the miracle. Man
|
||||
|
||||
After these words, it becomes more understandable, probably, that when mathematicians had a personal computer at their disposal, providing opportunities for computations on a previously unimaginable scale, they soon recalled the old mystery. As Mumford writes in the preface to their book, the temptation to use modern computer graphics to visibly see Klein's "absolutely unimaginable" tilings was irresistible…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
In recent decades, research in various fields of physics has shown that Klein's tilings are directly related to modern ideas about the behavior of chaotic self-similar systems, observed in statistical mechanics, phase transition research, and the study of turbulence in liquids and gases.
|
||||
|
||||
@ -686,9 +680,9 @@ Research confirmed that on any scale – from the very large to the microscopica
|
||||
|
||||
Having constructed with the help of a computer the final fractal drawing – the limit set of one of Klein's symmetric iterative procedures – the researchers, captivated by the beauty of the result, could not resist and gave it the lofty-poetic name "The Glowing Limit."
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
As often happens with deep and inspired research, at some stage of their work, scientists seem to accidentally stumble upon a very ancient imagery, surprisingly in tune with their own results.
|
||||
|
||||
@ -696,15 +690,15 @@ This symbol is called "Indra's Net" and permeates a well-known Buddhist work cal
|
||||
|
||||
Translated into English, the corresponding fragment of the sutra looks approximately like this:
|
||||
|
||||
In the heaven of the great god Indra is said to be a vast and shimmering net, finer than a spider's web, stretching to the outermost reaches of space. Strung at the each intersection of its diaphanous threads is a reflecting pearl. Since the net is infinite in extent, the pearls are infinite in number.
|
||||
|
||||
In the glistening surface of each pearl are reflected all the other pearls, even those in the furthest corners of the heavens. In each reflection, again are reflected all the infinitely many other pearls, so that by this process, reflections of reflections continue without end.
|
||||
> In the heaven of the great god Indra is said to be a vast and shimmering net, finer than a spider's web, stretching to the outermost reaches of space. Strung at the each intersection of its diaphanous threads is a reflecting pearl. Since the net is infinite in extent, the pearls are infinite in number.
|
||||
>
|
||||
> In the glistening surface of each pearl are reflected all the other pearls, even those in the furthest corners of the heavens. In each reflection, again are reflected all the infinitely many other pearls, so that by this process, reflections of reflections continue without end.
|
||||
|
||||
As the researchers themselves comment on this discovery, they found that the entire mathematical construct of Klein, including the identical structures infinitely repeating within each other on an ever-diminishing scale, astonishingly reproduces the philosophy and images of the "Avatamsaka Sutra."
|
||||
|
||||
Delving a bit into the legacy of Eastern wisdom, mathematicians found the following commentary on the corresponding fragment (in F. Cook's book "Hua-Yen Buddhism: The Jewel Net of Indra," [o73]):
|
||||
|
||||
> The Hua-yen school has been fond of this image, mentioned many times in its literature, because it symbolises a cosmos in which there is an infinitely repeated interrelationship among all the members of the cosmos. This relationship is said to be one of simultaneous mutual identity and mutual intercausality.
|
||||
> The Hua-yen school has been fond of this image, mentioned many times in its literature, because it symbolises a cosmos in which there is an infinitely repeated interrelationship among all the members of the cosmos. This relationship is said to be one of **simultaneous mutual identity and mutual intercausality**.
|
||||
|
||||
And another commentary from a knowledgeable expert – from Sir Charles Eliot [o74]:
|
||||
|
||||
@ -722,7 +716,7 @@ His article was titled "*The Dance of Shiva: The Hindu View of Matter in the Lig
|
||||
|
||||
Of course, long before Capra, many prominent theorists with sufficient erudition had noted the striking resonance of the nontrivial concepts of modern physics with the ideas of Hinduism, Buddhism, and Taoism. However, Fritjof Capra managed not only to gather these disparate observations but also to compile them into a unified picture that, over time, not only doesn't age but rather gains greater clarity and persuasiveness.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
Since modern science still lacks a clear understanding of how brilliant ideas and concepts are born in the minds of researchers, it will be useful to mention here some quite specific circumstances that prompted Capra to his interdisciplinary explorations and the writing of such a successful book. Here is how the author himself describes it in the preface to his work. [o76]
|
||||
|
||||
@ -732,9 +726,9 @@ That is, as a physicist, he, of course, already knew well that the sand and rock
|
||||
|
||||
Now, Capra felt all this directly: he "saw" cascades of energy coming down from outer space, in which particles were created and destroyed in rhythmic pulses; he "saw" the atoms of the elements and the atoms of his body participating in this cosmic dance of energy; he felt the rhythm and "heard" the sound of this dance. And he knew exactly what it was called – it was the dance of Shiva Nataraja, or the Lord of the Dancers, worshipped by the Hindus.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The canonical depiction of Shiva Nataraja, which clearly took shape in the bronze sculptures of the 10th–11th centuries, is now considered the most expressive and comprehensive symbol of Hinduism, portraying Shiva as the energy and life of all existence.
|
||||
|
||||
@ -756,13 +750,13 @@ In conclusion to this brief description, we can repeat the words of one of the a
|
||||
|
||||
> If a single image were needed to represent the extraordinarily rich and complex cultural heritage of India, Shiva Nataraja could be the most suitable candidate.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
For any attentive reader, it's probably already clear that the image of Shiva's cosmic dance is, one might say, a philosophical-poetic description of the same world model previously presented here in physical-mathematical terms and concepts, now in the anthropomorphic form of a Hindu deity.
|
||||
|
||||
If the idea of a direct correspondence of the images still seems murky and not at all obvious to the reader, it is beneficial to examine some of the main details of the Nataraja image, which are crucially important from a physics point of view. Primarily, the damaru drum is of interest, widely used in the religious music of Hinduism and Tibetan Buddhism.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The damaru is a small two-membrane percussion instrument played with just one hand. The body of the drum is made of wood in the shape of an hourglass — two cones with converging tips and bases covered with leather.
|
||||
|
||||
@ -774,7 +768,7 @@ Comparing the key details of the construct with the damaru's design, it is impos
|
||||
|
||||
In the rituals of Hinduism, it is believed that the damaru is a drum with a very special spiritual energy of influence, as it means the primal sound of the universe – "Para Nada." Moreover, according to legend, the language of sacred wisdom of the Hindus, Sanskrit, was initially conveyed to people in the rhythms of the sounds made by the damaru…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
As a matter of fact, regarding the transmission of knowledge through the vibrations of a drum membrane, there is another, much more modern, credible, and at the same time quite instructive story.
|
||||
|
||||
@ -792,7 +786,7 @@ Today, one can only speculate about the discoveries and achievements this expres
|
||||
|
||||
For reasons that remain unknown, the publishing house ignored the author's wishes and released his lectures with a simple red cover without any drawings. To acknowledge the author's ideas, they included an atypical photograph of the scientist in the preface — one where he is playing the drums… [o78]
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
It is well known that Richard Feynman, due to his character, paid extremely great attention to graphic symbolism. For example, he would send his car to a workshop for a special paint job to have "Feynman diagrams" painted on the sides. That is, one of the most important scientific achievements of the physicist, which, due to its powerful graphic component, became something of his signature.
|
||||
|
||||
@ -808,7 +802,7 @@ According to the recollections of colleagues and students, Heinz Hopf often aske
|
||||
|
||||
For Hopf personally, as known from his surroundings, the answer to such a question was absolutely clear: "No, never and under no circumstances." But as for his friend Pauli (and probably Richard Feynman, John von Neumann, and a number of other prominent scientists with significant connections in the circles of secret science of the US military-industrial complex), the answer to the question is far from clear…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
A crucial key to the mystery surrounding Wolfgang Pauli's main and undisclosed discovery is a phrase from his postcard to his old friend Werner Heisenberg: "Division and reduction of symmetry, this is the kernel of the brute!"
|
||||
|
||||
@ -834,7 +828,7 @@ Secondly, to start receiving it at any point in space, it is enough to take a cl
|
||||
|
||||
And thirdly — judging from the deafening silence surrounding some curious physical phenomena like the Hyde vacillation — it can be assumed that some secret scientific laboratories has long been in possession of such sources of free energy. Only it seems they absolutely do not want to share this happiness with the rest of humanity… (details see here: [i84][i85][i86][i87][i88]).
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
Exploring how far the deeply classified science of the USA has managed to go compared to the results of open world science may be an interesting matter, but in the absence of reliable facts, it is completely pointless.
|
||||
|
||||
@ -848,7 +842,7 @@ The most well-known of these gods, Quetzalcoatl or "Feathered Serpent" in litera
|
||||
|
||||
The image of another god, named Tezcatlipoca or "Smoking Mirror," is directly related to the creation of the world, in its functions most closely akin to the image of Shiva in Hinduism, thus can appear both in wrathful and benevolent guises — like nature itself.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
One of the most important features of the image of Tezcatlipoca is his pronounced asymmetry: the god has only a left leg, while in place of the second, right leg, he is depicted either with a mirror or a serpent. The significant cosmic role of the mirror and the general notion of the universe as a “hall of mirrors” are, it is worth noting, characteristic of the Hua-yen school of Buddhism [i89], and in modern science — of the dodecahedral model by Jean-Pierre Luminet and Jeffrey Weeks. [i90]
|
||||
|
||||
@ -858,13 +852,13 @@ Although there was also a fourth brother, Xipe Totec (whose name is better decip
|
||||
|
||||
A characteristic feature in the image of all four brothers, who created the world, was that each had a round ring, or "symbol of eternity" and the closed nature of space-time, suspended from their chest with a ribbon.
|
||||
|
||||
In this regard, to clearly correlate the symbolism of the ancient religion with the history of modern physics, one can recall the "Great Vision of the Clocks of the World" by Wolfgang Pauli [i82]. And at the same time, decode the last unsolved detail of this dream.
|
||||
In this regard, to clearly correlate the symbolism of the ancient religion with the history of modern physics, one can recall the "Great Vision of the World Clock" by Wolfgang Pauli [i82]. And at the same time, decode the last unsolved detail of this dream.
|
||||
|
||||
The horizontal circle of the dial in the clocks of the universe was divided into four sectors, each of which had its own color. In each sector stood a human figure holding a pendulum — the symbol of the eternal movement of the clocks of the world…
|
||||
|
||||
And one more — topological — nuance on the same theme. In the developed dodecahedral model of the universe, representing the construction of the cosmos in the form of a twin soccer ball, there is one specific feature. Two surfaces of the Riemann sphere, nested within one another, are topologically equivalent to one surface of a torus because the "ball" structure has four pinched holes — "four cardinal directions" or four corners of the globe — ensuring the unity (meaning a single surface) of the doubled world… [i91]
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
In attempts to digest all the knowledge about the nature of the world that ancient wise men gained without formulas — just like that, through meditation and reflection — modern scientists will inevitably want to raise some objections. Like that "perhaps there were clever people among them, of course, but look at what it all resulted in — only religious obscurantism and piles of corpses in bloody sacrifices to their gods"…
|
||||
|
||||
@ -874,7 +868,7 @@ To finish the chapter on a positive note, it's much nicer to talk about a signif
|
||||
|
||||
In the summer of 2004, on the grounds of CERN, the European Organization for Nuclear Research near Geneva, a two-meter statue of Shiva Nataraja was ceremoniously installed as a gift from the Indian government to commemorate many years of fruitful cooperation with European scientists.
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
Inscribed on the pedestal of the statue are words from Fritjof Capra’s book The Tao of Physics — about Shiva’s cosmic dance as a metaphor of universal significance:
|
||||
|
||||
@ -888,9 +882,7 @@ Our visible part of the universe on the sculpture is just the circle of light fr
|
||||
|
||||
For this reason, perhaps the most important element of the sculpture today should be considered Shiva's calming and encouraging gesture – "Abhaya Hasta." That is, "do not fear, friends," those who possess true knowledge have none and nothing to fear – in literally all respects…
|
||||
|
||||
<center></center>
|
||||
|
||||
It makes sense to compare the canonical drawing on Shiva's palm with the image of "the glowing limit" from the book of Mumford, Siris, and Wright.
|
||||

|
||||
|
||||
<center>(64)</center>
|
||||
|
||||
@ -906,7 +898,7 @@ The brief answer to this question boils down to the fact that civilizations and
|
||||
|
||||
For a slightly more detailed perspective on the history and essence of our constant – and often close family – contacts with aliens, it is more convenient to resort to metaphor.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
The tremendous success with the public that James Cameron's film "Avatar" achieved is commonly explained by a multitude of various reasons – long and thoroughly examined by both art critics and entertainment market analysts.
|
||||
|
||||
@ -922,13 +914,13 @@ Without delving into the depths of all these parallels, let us touch only on the
|
||||
|
||||
It is clear that Cameron did not invent this trick himself but borrowed both its essence and its name from the boundlessly rich culture of Hinduism. Where for thousands of years the religious tradition has operated with the idea of the "descent" of their gods to people in the guise of one or another avatar.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
Particularly of historical interest in this context are the so-called "cultural heroes" in the myths of practically all peoples of the planet Earth. That is, beneficent figures who appear in one way or another and bestow on primitive tribes, dwelling in the darkness of ignorance, the most diverse knowledge and skills – from making fire and sowing grains to the skills of writing and accounting.
|
||||
|
||||
As a particularly impressive example of such enlightening activities, it is worth recalling a character called the god Thoth or Djehuty – revered as the founder of all, essentially, intellectual life of Ancient Egypt. It is worth mentioning that he was depicted as a man with the head of an ibis bird (a symbol of the shining pure mind Akh).
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
The cult of the wisest god Thoth, according to historical evidence, was one of the most ancient on the entire territory of the Egyptian state. Since in each region – or nome – of Egypt it was customary to particularly revere one of the deities of their extensive pantheon, the center of worship for Thoth was the capital of the 15th nome, the city of Hermopolis, or Khemenu, famous throughout the country for its richest library.
|
||||
|
||||
@ -938,7 +930,7 @@ All these "chapters" (a more correct translation might be "spells") of this coll
|
||||
|
||||
For a modern person, absolutely distant from the religious beliefs of the Egyptians, practically all these texts now represent perhaps only a purely historical interest. But there is one absolutely remarkable exception, which is called "Chapter 64, or the Chapter of Knowing the Chapters of Coming Forth by Day in a Single Chapter"…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
Both the name itself and the explanations of the ancient commentators of chapter 64 leave no doubt that this text, in its essence, represented a kind of summary of all the other "Chapters on the Ascent to the Light" and in itself held no less value than all the other chapters combined.
|
||||
|
||||
@ -954,14 +946,14 @@ In the following millennia, when including the text of such a marvelous chapter
|
||||
|
||||
"If the deceased will know this Chapter, he will ascend to the light, and at none of the gates of the Duat (afterlife) will he encounter resistance, whether when exiting it or when entering."
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
Finally, after such an intriguing preamble, it is time to present an almost verbatim translation of the text of "Chapter 64" (for better understanding noting that in ancient times the disk of the sun, which bestows light and life, was referred to as the "Lion-god"):
|
||||
|
||||
> I am the day yesterday, and the day today, and the day tomorrow. And I am able to be reborn into new life.
|
||||
|
||||
I am the divine hidden soul, who creates the gods and who gives meals to the divine hidden beings.
|
||||
|
||||
>
|
||||
> I am the divine hidden soul, who creates the gods and who gives meals to the divine hidden beings.
|
||||
>
|
||||
> I am the possessor of two divine faces, I , who comes forth from out of the darkness.
|
||||
>
|
||||
> I greet you, two divine Hawks, sitting in your nests and listening to the words.
|
||||
@ -971,14 +963,14 @@ I am the divine hidden soul, who creates the gods and who gives meals to the div
|
||||
> I am the maker of my name. The closed door in the wall has been broken, and that which previously inspired fear has been overthrown and discarded.
|
||||
>
|
||||
> The mighty god has regained his eye, his face radiates light, my name – is his name. I will not undergo decay, but will gain new birth in the form of the Lion-god. I am the lord of my life.
|
||||
>
|
||||
> I have come to see him that dwelleth in his divine serpent, face to face and eye to eye.
|
||||
>
|
||||
> O Lion-god, you dwell in me, and I in you; and your attributes are my attributes.
|
||||
>
|
||||
> I have entered in as a man of no understanding, and I shall ascend to the light in the form of a strong Spirit, and and I will look at my embodiments, male and female, for eternity…
|
||||
|
||||
I have come to see him that dwelleth in his divine serpent, face to face and eye to eye.
|
||||
|
||||
O Lion-god, you dwell in me, and I in you; and your attributes are my attributes.
|
||||
|
||||
I have entered in as a man of no understanding, and I shall ascend to the light in the form of a strong Spirit, and and I will look at my embodiments, male and female, for eternity…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
On this uplifting note, it is best to pause with reading and listen carefully to oneself. And – if not touched – perhaps reread the Chapter of Thoth with attention once again. All people are, of course, different, but each of us has our own "two birds" in the nests inside – and at such moments of contact with the truth, all three levels of our Self are most ready for contact…
|
||||
|
||||
@ -994,7 +986,7 @@ Interestingly, around the same time (a few years later), Pauli's friend and fell
|
||||
|
||||
What is remarkable is that in this dream, the guests tried to demonstrate clearly to the scholar that it is "they" who project "us," and not the other way around (as Jung publicly declared UFOs to be "projections" of our own restless mind).
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
A notable nuance in this storyline with Dr. Jung is how exactly our contacts with "alien intelligence" are happening now — when the guests mostly come to us "from within," on other levels of reality, rather than "from outside," in visually observable forms.
|
||||
|
||||
@ -1006,7 +998,7 @@ Naturally, as with any other communication system, not all information received
|
||||
|
||||
Because the essence of the process is about a person understanding very simple, but still not obvious truths. About the fact that every person is actually much, incomparably much more than we see in the mirror. About how the universe is literally permeated with life and intelligence everywhere. And finally, about how the mind of every person is inextricably integrated into this single whole…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
But if the entire vast universe is life and intelligence in their infinitely diverse manifestations, then why (someone might ask) would all these hypothetical crowds of invisible aliens be hanging around our tiny and out-of-the-way planet?
|
||||
|
||||
@ -1020,7 +1012,7 @@ Explaining the essence of the intrigue in the briefest terms, practically all fo
|
||||
|
||||
On planet Earth, they say that a long time ago, it was about the same as everywhere else. But some spiritually underdeveloped colonizers living on a higher level became so engrossed in games of power that the life on the planet was nearly destroyed. And in order to cut off the natives from the adverse influence of all such "gods and demons" for the future, it was decided to slightly modify our DNA — by blocking direct communication with all the floors of consciousness above the second chakra.
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
On one hand, this demoted ancient Homo sapiens to the level of an animal whose consciousness is concerned only with biological survival. But from another perspective, we gained the opportunity for an independent, truly personal evolution.
|
||||
|
||||
@ -1038,7 +1030,7 @@ Or, for example, why certain races of aliens are now abundantly and quite persis
|
||||
|
||||
Finally, this perspective clarifies much more distinctly why we are all so amazingly different on this planet. And why it is still so difficult for us to finally agree on a peaceful and calm life among ourselves…
|
||||
|
||||
<center>*</center>
|
||||
<center>#</center>
|
||||
|
||||
The theme of peace on Earth is immeasurably more important and relevant than any plots about alien presence. Simply because all invisibly present ET races here have already learned — unlike us — to manage without military conflicts, one way or another.
|
||||
|
||||
@ -1048,9 +1040,7 @@ In other words, no new "colonizer invasion" threatens us anymore. While we were
|
||||
|
||||
There is only one thing that inspires hope. Most normal representatives of humanity do clearly acknowledge what madness war is. And only we ourselves can and must stop this madness. In connection with which it seems more than appropriate to choose such a wonderful symbol as "The World in Our Hands" as the finale.
|
||||
|
||||
<center></center>
|
||||
|
||||
http://glendahecksher.com.mx/
|
||||

|
||||
|
||||
The author of this monument, where the shadow from two folded hands forms a giant peace bird on the ground, is the Mexican artist and sculptor Glenda Hecksher. It is also worth mentioning this sculpture, adorning one of Mexico City's squares, for one highly significant reason.
|
||||
|
||||
@ -1066,7 +1056,7 @@ There are quite a few ways to wake up. One of the simplest recipes has been form
|
||||
|
||||
<center>THE END</center>
|
||||
|
||||
<center></center>
|
||||

|
||||
|
||||
### Inside links
|
||||
|
||||
|
||||
@ -22,6 +22,7 @@
|
||||
}
|
||||
|
||||
figure {
|
||||
text-align: center;
|
||||
margin-left: 0;
|
||||
margin-right: 0;
|
||||
.img-wrapper {
|
||||
|
||||
@ -33,19 +33,20 @@ class TZO
|
||||
public function getPartHtml(int $n): string {
|
||||
$markdown_file = APP_ROOT.'/data/tzo/'.$n.'.md';
|
||||
$md = file_get_contents($markdown_file);
|
||||
$html = MarkupUtil::markdownToHtml($md,
|
||||
use_image_previews: false);
|
||||
|
||||
$html = preg_replace_callback(
|
||||
// images
|
||||
$md = preg_replace_callback(
|
||||
'#!\[]\('
|
||||
.'(https://kniganews\.org/wp-content/uploads/(\d{4})/(\d{2})/([^/\s]+))' // 1=url, 2=year,3=month,4=filename
|
||||
.'(?:\s+"([^"]*)")?' // 5=caption (optional)
|
||||
.'\)#',
|
||||
// 1=url, 2=year, 3=month, 4=filename
|
||||
. '(https://kniganews\.org/wp-content/uploads/(\d{4})/(\d{2})/([^/\s]+))'
|
||||
// 5=caption: either a backslash+any-char, or anything but " or \
|
||||
. '(?:\s+"((?:\\\\.|[^"\\\\])*)")?'
|
||||
. '\)#',
|
||||
function($m) {
|
||||
$year = $m[2];
|
||||
$month = $m[3];
|
||||
$filename = $m[4];
|
||||
$caption = $m[5] ?? '';
|
||||
$caption = isset($m[5]) ? stripcslashes($m[5]) : '';
|
||||
$new_file = $year.$month.'_'. $filename;
|
||||
$path = APP_ROOT.'/public/ic/images/tzo/'.$new_file;
|
||||
list($w, $h) = $this->getImageSize($path); // TODO cache image size
|
||||
@ -56,9 +57,12 @@ class TZO
|
||||
.'</figure>'
|
||||
);
|
||||
},
|
||||
$html
|
||||
$md
|
||||
);
|
||||
|
||||
$html = MarkupUtil::markdownToHtml($md,
|
||||
use_image_previews: false);
|
||||
|
||||
// links
|
||||
$html = preg_replace_callback(
|
||||
'/<center>\s*\(\[([^]]+)\]\(([^)]+)\)\)\s*<\/center>/',
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user